Depth First Search (DFS) – Iterative and Recursive Implementation #
Depth–first search (DFS) is an algorithm for traversing or searching tree or graph data structures. One starts at the root (selecting some arbitrary node as the root for a graph) and explore as far as possible along each branch before backtracking.
Introduction #
The following graph shows the order in which the nodes are discovered in DFS:
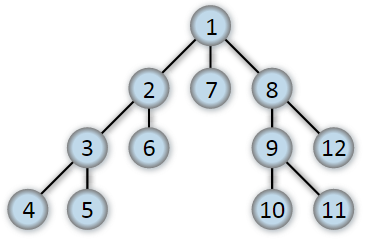
Depth–first search in trees #
A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any acyclic connected graph is a tree. For a tree, we have the following traversal methods:
- Preorder: visit each node before its children.
- Postorder: visit each node after its children.
- Inorder (for binary trees only): visit left subtree, node, right subtree.
These are already covered in detail in separate posts.
Depth–first search in Graph #
A Depth–first search (DFS) is a way of traversing graphs closely related to the preorder traversal of a tree. Following is the recursive implementation of preorder traversal:
procedure preorder(treeNode v)
{
visit(v);
for each child u of v
preorder(u);
}
To turn this into a graph traversal algorithm, replace “child” with “neighbor”. But to prevent infinite loops, keep track of the vertices that are already discovered and not revisit them.
procedure dfs(vertex v)
{
visit(v);
for each neighbor u of v
if u is undiscovered
call dfs(u);
}
Recursive Implementation of DFS #
The recursive algorithm can be implemented as follows in C++:
#include <iostream>
#include <vector>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Function to perform DFS traversal on the graph on a graph
void DFS(Graph const &graph, int v, vector<bool> &discovered)
{
// mark the current node as discovered
discovered[v] = true;
// print the current node
cout << v << " ";
// do for every edge (v, u)
for (int u: graph.adjList[v])
{
// if `u` is not yet discovered
if (!discovered[u]) {
DFS(graph, u, discovered);
}
}
}
int main()
{
// vector of graph edges as per the above diagram
vector<Edge> edges = {
// Notice that node 0 is unconnected
{1, 2}, {1, 7}, {1, 8}, {2, 3}, {2, 6}, {3, 4},
{3, 5}, {8, 9}, {8, 12}, {9, 10}, {9, 11}
};
// total number of nodes in the graph (labelled from 0 to 12)
int n = 13;
// build a graph from the given edges
Graph graph(edges, n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n);
// Perform DFS traversal from all undiscovered nodes to
// cover all connected components of a graph
for (int i = 0; i < n; i++)
{
if (discovered[i] == false) {
DFS(graph, i, discovered);
}
}
return 0;
}
Output: 0 1 2 3 4 5 6 7 8 9 10 11 12
The time complexity of DFS traversal is O(V + E), where V and E are the total number of vertices and edges in the graph, respectively. Please note that O(E) may vary between O(1) and O(V2), depending on how dense the graph is.
Iterative Implementation of DFS #
The non-recursive implementation of DFS is similar to the non-recursive implementation of BFS but differs from it in two ways:
- It uses a stack instead of a queue.
- The DFS should mark discovered only after popping the vertex, not before pushing it.
- It uses a reverse iterator instead of an iterator to produce the same results as recursive DFS.
Following is the C++
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Perform iterative DFS on graph starting from vertex `v`
void iterativeDFS(Graph const &graph, int v, vector<bool> &discovered)
{
// create a stack used to do iterative DFS
stack<int> stack;
// push the source node into the stack
stack.push(v);
// loop till stack is empty
while (!stack.empty())
{
// Pop a vertex from the stack
v = stack.top();
stack.pop();
// if the vertex is already discovered yet,
// ignore it
if (discovered[v]) {
continue;
}
// we will reach here if the popped vertex `v` is not discovered yet;
// print `v` and process its undiscovered adjacent nodes into the stack
discovered[v] = true;
cout << v << " ";
// do for every edge (v, u)
// we are using reverse iterator (Why?)
for (auto it = graph.adjList[v].rbegin(); it != graph.adjList[v].rend(); it++)
{
int u = *it;
if (!discovered[u]) {
stack.push(u);
}
}
}
}
int main()
{
// vector of graph edges as per the above diagram
vector<Edge> edges = {
// Notice that node 0 is unconnected
{1, 2}, {1, 7}, {1, 8}, {2, 3}, {2, 6}, {3, 4},
{3, 5}, {8, 9}, {8, 12}, {9, 10}, {9, 11}
// {6, 9} introduces a cycle
};
// total number of nodes in the graph (labelled from 0 to 12)
int n = 13;
// build a graph from the given edges
Graph graph(edges, n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n);
// Do iterative DFS traversal from all undiscovered nodes to
// cover all connected components of a graph
for (int i = 0; i < n; i++)
{
if (discovered[i] == false) {
iterativeDFS(graph, i, discovered);
}
}
return 0;
}
Output: 0 1 2 3 4 5 6 7 8 9 10 11 12