Distributed system concepts #
A learning notes extracted from MIT 6.824 Lecture 3 and Lecture 8.
The contradictory loop #
Often the starting point for people designing big distributed system or big storage system is that they want to get huge aggregated performance and harness the resources of hundreds of machines in order to get a huge amount of work done.
So, the natural next thought is to split the data over a huge number of servers in order to read/write many servers in parallel, this split process is called sharding or partitioning.
However, if we shard data over many servers we will see constant faults, i.e., if we have hundreds of thousands of servers there is always gonna be one down. So we need an automatic fault-tolerance system. Among the most powerful ways to get fault tolerance is with replication, e.g., we keep 2 or 3 copies of the data and if one of them fails we can use another one.
Now, if we have replication, say two copies of data, then they will get out of sync without careful design, so what you thought was to replicas the data where you can use either one of the data interchangeablely to tolerate the faults. if you are not careful, you will end up with two almost identical replicas of the data that are not exactly replicas at all, and what you get back depends on which one you talk to, that’s starting to look a little bit tricky for applications to use.
So, if we have replication, we risk weird inconsistencies. To get rid of inconsistency and make the data look very well-behaved, it almost always extra work and extra chitchat between all the different servers and clients in the network that reduce performance.
Finally, if we want consistency, we pay for low performance, which is of course not what we originally hoped for. This is where the contradictory loop formed, i.e.,
high performance -> shard data over many servers
many servers -> constant faults
fault tolerance -> replication
replication -> potential inconsistencies
better consistency -> low performance
Of course, this isn’t absolute, you can build very high-performance systems, but nevertheless, there is this sort of inevitable way that the design of these systems plays out and it results in a tension between the original goals of performance and the sort of realization that if you want good consistency you are gonna pay for it and if don’t want to pay for it, you have to suffer with anomalous behavior.
So in the design of the distributed system, we will see this loop many times, different systems would have different tradeoffs between the performance and the consistency.
What does consistency means #
The ideal consistency model would behave as a single server, for example, a single server use attached disk as the storage, and executes client operation one at a time(even if concurrent), the reads will reflect previous writes even if server crashes and restarts.
With this single server model, suppose the following example in Figure 1: C1 and C2 write x concurrently, and after the writes have completed, C3 and C4 read x. what can they see?
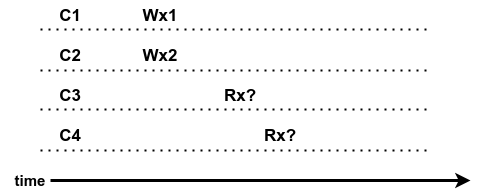 |
|---|
| Figure 1: An example question for strong consistency, in which, Wx1 means write x with value 1, same for Wx2, write x with value 2, Rx means Read x |
The answer is: either 1 or 2, but both have to see the same value.
This is a strong consistency model. But a single server has poor fault-tolerance.
However, the Replication for fault-tolerance makes strong consistency tricky. Here is a simple but broken replication schema in Figure 2:
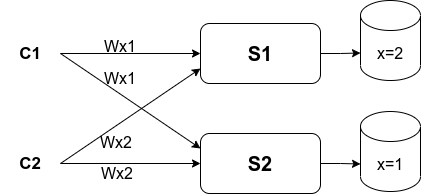 |
|---|
| Figure 2: A bad replication example, In which, there are two servers, each with a complete copy of the data, we want to keep these copies identical so that if one server fails we can read or write from another server. That means somehow every write must be processed by both servers and reads have to be processed by a single server otherwise it’s not fault-tolerant, in other words, if reads have to consult both then we can’t survive the loss of one of the servers. let’s suppose we have C1 and C2, and they both want to write mentioned in Figure 1, i.e., C1 writes x to 1, and C2 writes x to 2, so C1 will launch Wx1 to both servers because we want to update both of them, same for C2 |
The problem comes up when C1’s and C2’s write messages arrive in different orders at the two replicas, for our example, S1 process Wx1 then Wx2, whereas, S2 process Wx2 first and Wx1 second.
- If C3 reads S1, it will see x=2
- If C4 reads S2, it will see x=1
Some other situations could lead to inconsistency problems as well, for example, if S1 receives a write but the client crashes before sending the write to S2.
Linearizability #
In order to tell how should clients expect Write/Put and Read/Get to behave, we sort of need a consistency contract, which defines the correctness of a distributed system, and helps us reason about how to handle complex situations correctly, e.g., concurrency, replicas, failures, RPC retransmission, leader changes, optimizations.
The linearizability is the most common and intuitive definition that formalizes behavior expected of a single server(strong consistency).
linearizability definition: an execution history is linearizable if
- one can find a total order of all operations,
- that matches real-time(for non-overlapping/non-concurrent ops), and
- in which each read sees the value from the write preceding it in the order(most recent data in the order).
Notes:
- A history is a record of client operations, each with arguments, return value, time of start, and time completed.
- The definition is based on external behavior so we can apply it without having to know how service works
- Histories explicitly incorporate concurrency in the form of overlapping operations(multiple ops don’t occur at a point in time), thus a good match for how distributed systems operate.
Let’s take some examples for explanations, we use the following annotations in the examples:
- “Wx1” means “write value 1 to record x”
- “Rx1” means “a read of record x yielded value 1”
- Whenever there is overlap in terms of the operation time duration, it means the operations occur concurrently, and the outcome order of these operations can be either way, e.g., if Wx1 and Wx2 are overlapping, either Wx1 -> Wx2 or Wx2 -> Wx1 are both valid outcome order of operations.
Example history 1
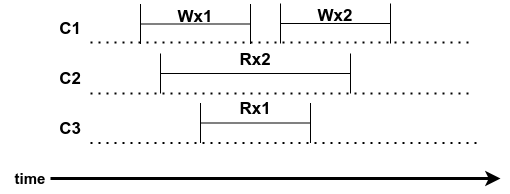 |
|---|
| Figure 3: Example history 1, linearizable with order Wx1 Rx1 Wx2 Rx2 |
Example history 2
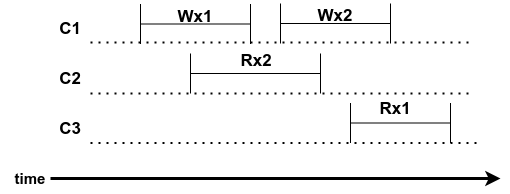 |
|---|
| Figure 4: Example history 2, Not linearizable |
From the history, we can observe that Wx1 -> Wx2 in real-time, if C2 gets Rx2, it means Wx1 must happened already, which means, C3 can NOT get Rx1 in a linearizable system. In other words, there is a cycle formed shown in figure 5
 |
|---|
| Figure 5: Example history 2, operation cycle found |
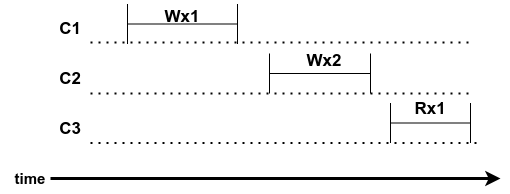
Example history 3
 |
|---|
| Figure 6: Example history 3 |
We can found a total order of all operations: Wx0 Wx2 Rx2 Wx1 Rx1, so the history is linearizable,
Takeway:
- the service can pick either order for concurrent writes.
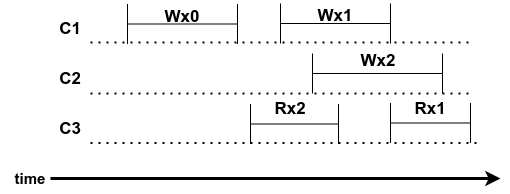
Example history 4
 |
|---|
| Figure 7: Example history 4 |
What are the constraints?
- Wx2 then C3: Rx2 (value)
- C3: Rx2 then Wx1 (value)
- Wx1 then C4: Rx1 (value)
- C4: Rx1 then Wx2 (value)
There is a cycle found shown in figure 7:
 |
|---|
| Figure 8: Example history 4, opeartion cycle found |
Takeways:
- service can choose either order for concurrent writes
- but all clients must see the writes in the same order, this is important when we have replicas or caches they have to all agree on the order in which operations occur
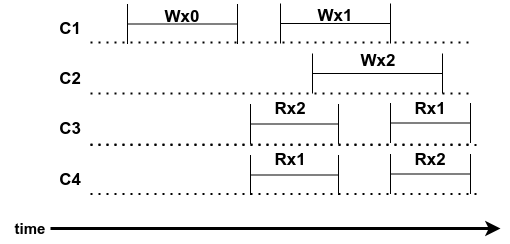
Example history 5:
 |
|---|
| Figure 9: Example history 5 |
The constraints in the example are
- Wx2 before Rx1 (time)
- Rx1 before Wx2 (value)
So, there is a cycle, not linearizable, and the time constraints means only possible is Wx1 Wx2 Rx1
Takeways:
- reads must return fresh data: stale values aren’t linearizable
- even if the reader doesn’t know about the write, the time rule requires reads to yield the latest data
- linearzability forbids many situations: split brain (two active leaders), forgetting committed writes after a reboot, reading from lagging replicas and so on.
Example history 6:
Suppose clients re-send requests if they don’t get a reply in case it was the response that was lost:
- leader remembers client requests it has already seen
- if sees dupliate, replies with saved response from first execution
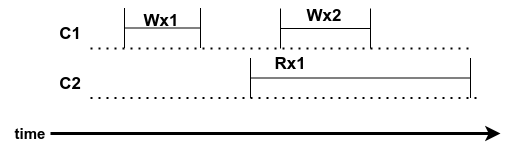 |
|---|
| Figure 10: Example history 6 |
The example yield a saved value from long agao(a stale value) with order Wx1 Rx1 Wx2
Takeways:
- By following the linearizability rules, returning the stale value is correct in case of client retry.
- In our example, C1 getting Rx2 would be correct as well because Wx2 and Rx1 are considered two current operations
Linearizability versus Serializability #
Linearizability and serializability are both important properties about interleavings of operations in databases and distributed systems, and it’s easy to get them confused.
Linearizability #
The main takeways of linearizablility are: single-operation, single-object, real-time order
Linearizability is a guarantee about single operations on single objects. It provides a real-time (i.e., wall-clock) guarantee on the behavior of a set of single operations (often reads and writes) on a single object (e.g., distributed register or data item).
In plain English, under linearizability, writes should appear to be instantaneous. Imprecisely, once a write completes, all later reads (where “later” is defined by wall-clock start time) should return the value of that write or the value of a later write. Once a read returns a particular value, all later reads should return that value or the value of a later write.
Linearizability for read and write operations is synonymous with the term “atomic consistency” and is the “C,” or “consistency,” in Gilbert and Lynch’s proof of the CAP Theorem. We say linearizability is composable (or “local”) because, if operations on each object in a system are linearizable, then all operations in the system are linearizable.
Serializability #
The main takeways of linearizablility are: multi-operation, multi-object, arbitrary total order
Serializability is a guarantee about transactions, or groups of one or more operations over one or more objects. It guarantees that the execution of a set of transactions (usually containing read and write operations) over multiple items is equivalent to some serial execution (total ordering) of the transactions.
Serializability is the traditional “I,” or isolation, in ACID. If users’ transactions each preserve application correctness (“C,” or consistency, in ACID), a serializable execution also preserves correctness. Therefore, serializability is a mechanism for guaranteeing database correctness
Unlike linearizability, serializability does not—by itself—impose any real-time constraints on the ordering of transactions. Serializability is also not composable. Serializability does not imply any kind of deterministic order—it simply requires that some equivalent serial execution exists.
Strict Serializability #
Combining serializability and linearizability yields strict serializability: transaction behavior is equivalent to some serial execution, and the serial order corresponds to real time. For example, say I begin and commit transaction T1, which writes to item x, and you later begin and commit transaction T2, which reads from x. A database providing strict serializability for these transactions will place T1 before T2 in the serial ordering, and T2 will read T1’s write. A database providing serializability (but not strict serializability) could order T2 before T1
linearizability can be viewed as a special case of strict serializability where transactions are restricted to consist of a single operation applied to a single object.
Note:
One of the reasons these definitions are so confusing is that linearizability hails from the distributed systems and concurrent programming communities, and serializability comes from the database community. Today, almost everyone uses both distributed systems and databases, which often leads to overloaded terminology (e.g., “consistency,” “atomicity”).