Reb-Black Tree #
Reb-Black tree basic concept and operations.
Indroduction #
A red-black tree is a kind of self-balancing binary search tree where each node has an extra bit, and that bit is often interpreted as the color (red or black). These colors are used to ensure that the tree remains balanced during insertions and deletions. Although the balance of the tree is not perfect, it is good enough to reduce the searching time and maintain it around O(log n) time, where n is the total number of elements in the tree. This tree was invented in 1972 by Rudolf Bayer.
It must be noted that as each node requires only 1 bit of space to store the color information, these types of trees show identical memory footprints to the classic (uncolored) binary search tree.
Implementation #
https://github.com/maxnilz/tree/tree/main/rbtree
Visualization #
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
Properties #
In addition to the requirements imposed on a binary search tree the following must be satisfied by a red–black tree
- Every node is either red or black.
- All NIL nodes are considered black.
- There are no two adjacent red nodes (A red node cannot have a red parent or red child).
- Every path from a node (including root) to any of its descendants NIL nodes has the same number of black nodes.
The read-only operations, such as search or tree traversal, do not affect any of the requirements. On the other hand, the modifying operations insert and delete easily maintain requirements 1 and 2, but with respect to the other requirements some extra effort has to be taken, in order to avoid the introduction of a violation of requirement 3, called a red-violation, or of requirement 4, called a black-violation.
Why Red-Black Trees? #
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log n) after every insertion and deletion, then we can guarantee an upper bound of O(log n) for all these operations. The height of a Red-Black tree is always O(log n) where n is the number of nodes in the tree.
Comparison with AVL Tree #
The AVL Tree are more balanced compared to Red-Black Tree, but they may cause more rotations during insertion and deletion. So if your application involves frequent insertions and deletions, then Red-Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over the Red-Black Tree.
Rotations #
Before discussing Insertion and Deletion operations, we need to define the two basic rotations for reblancing the tree.
- Left Rotation
- Right Rotation
The rotation works precisely like the AVL tree.
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Insertion #
In AVL tree insertion we use rotation as a tool to do balancing after insertion, In the Red-Black tree, we use Rotation and Recoloring as the tools to do the balancing.
Recolouring is the change in colour of the node i.e. if it is red then change it to black and vice versa. It must be noted that the colour of the NIL node is always black. Moreover, we always try recolouring first, if recolouring doesn’t work, then we go for rotation. Following is a detailed algorithm. The algorithms have mainly two cases depending upon the colour of the uncle. If the uncle is red, we do recolour. If the uncle is black, we do rotations and/or recolouring.
Let the newly inserted node be N, P is used for N’s parent, G for the grandparent, and U will denote N’s uncle.
- Perform standard BST insert for N.
- Color the new node w as red intinally
- Perform repair process to fix the Red-Black tree
properties
During the repair, we have the following cases to consider:
| Case Name | P | G | U | x |
|---|---|---|---|---|
| I3 | NIL | |||
| I1 | ⚫ | |||
| I4 | 🔴 | NIL | ||
| I2 | 🔴 | ⚫ | 🔴 | |
| I5 | 🔴 | ⚫ | ⚫ | i |
| I6 | 🔴 | ⚫ | ⚫ | o |
Note, column x indicate the shape from G to N
- i is an inner granchild of G, it means the path from G to N forms a triangle
- o is an outer grandchild of G, it means the path from G to N forms a line
Insert case 1 #
The current node’s parent P is black, so requirement 3 holds. Requirement 4 holds as well.
Insert case 2 #
If both the parent P and the uncle U are red, then both of them can be repainted black and the grandparent G becomes red for maintaining requirement 4. Since any path through the parent or uncle must pass through the grandparent, the number of black nodes on these paths has not changed. However, the grandparent G may now violate requirement 3, if it has a red parent. Recursive repair on the higher level is required, i.e., let N := P and continue the repair process until the new N is root.
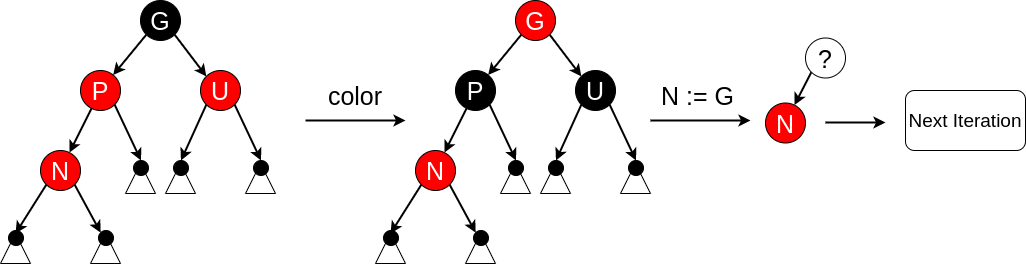
Insert case 3 #
The current node N is the (red) root of the tree, and all RB-properties are satisfied.
Insert case 4 #
The parent P is red and the root. Because N is also red, requirement 3 is violated. But after switching P’s color the tree is in RB-shape
Insert case 5 #
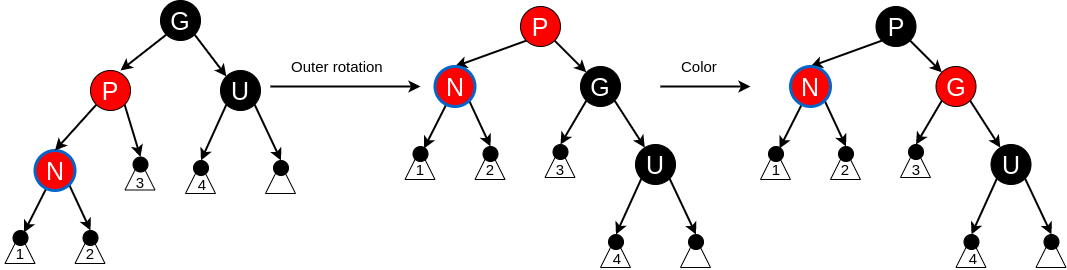
The parent P is red but the uncle U is black. The ultimate goal is to rotate the parent node P to the grandparent position, but this will not work if N is an “inner” grandchild of G (i.e., if N is the left child of the right child of G or the right child of the left child of G). A rotation at P switches the roles of the current node N and its parent P. The rotation adds paths through N (those in the subtree labeled 2, see diagram) and removes paths through P (those in the subtree labeled 4). But both P and N are red, so requirement 4 is preserved. Requirement 3 is restored in case 6.
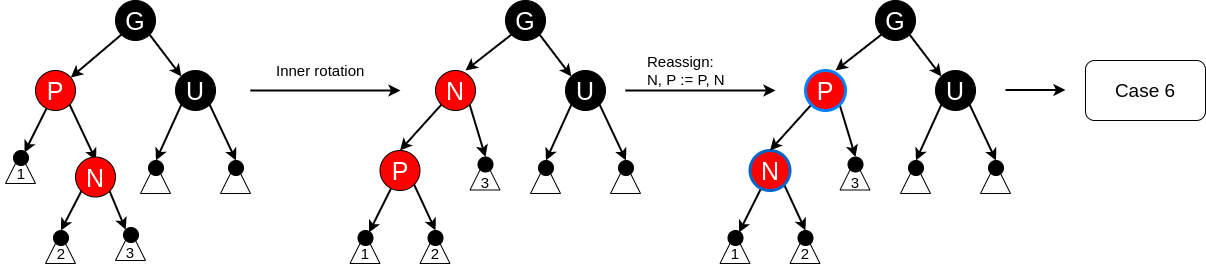
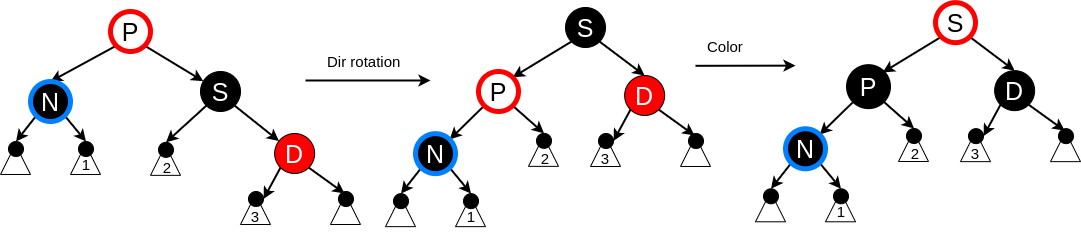
Insert case 6 #
The current node N is now certain to be an “outer” grandchild of G (left of left child or right of right child). Now (1-dir)-rotate at G, putting P in place of G and making P the parent of N and G. G is black and its former child P is red, since requirement 3 was violated. After switching the colors of P and G the resulting tree satisfies requirement 3. Requirement 4 also remains satisfied, since all paths that went through the black G now go through the black P.
Deletion #
Like Insertion, recoloring and rotations are used to maintain the Red-Black properties. In the insert operation, we check the color of the uncle to decide the appropriate case. In the delete operation, we check the color of the sibling to decide the appropriate case. The main property that violates after insertion is two consecutive reds. In delete, the main violated property is, change of black height in subtrees as deletion of a black node may cause reduced black height in one root to leaf path.
Like BST delete, delete node from RB tree needs to perform standard BST delete to find the Node to be deleted. When we perform standard delete operation in BST, we always end up deleting a node that have at most one non-NIL child, because the standard BST delete for the internal node requires to find inorder successor of the node and copy contents of the inorder successor to the node and delete the inorder successor.
Let the label N denotes the current node to be deleted, P is used for N’s parent, S for the sibling of N, C (meaning close nephew) for S’s child in the same direction as N, and D (meaning distant nephew) for S’s other child
Deletion: simple cases #
The deleting node N can have at most ONE non-NIL child.
- if
Nis the root that does not have a non-NIL child, it is replaced by a NIL node, after which the tree is empty—and in RB-shape. - If
Nhas exactly one non-NIL child, it must be a red child, because if it were a black one then requirement 4 would force a second black non-NIL child, therefore,Nitself must be black. As a consequence, the black nodeNcan be removed directly then have the `non-NIL red child node as the replacement and repaint it to black. - if
Ndoes not have a non-NIL child and it is red. As a consequence, the red nodeNcan simply be removed. - if
Ndoes not have a non-NIL child and it is black. i.e.,a black non-root leaf, 6 cases need to be taken care of.
Deletion of a black non-root leaf #
During the repair, we have the following cases to consider:
| Case Name | P | C | S | D |
|---|---|---|---|---|
| D2 | NIL | |||
| D3 | ⚫ | ⚫ | 🔴 | ⚫ |
| D1 | ⚫ | ⚫ | ⚫ | ⚫ |
| D4 | 🔴 | ⚫ | ⚫ | ⚫ |
| D5 | ⭕ | 🔴 | ⚫ | ⚫ |
| D6 | ⭕ | ⚫ | 🔴 |
Note, ⭕ indicate the node is either red or black.
Delete case 1 #
P, S, and S’s children are black. After painting S red all paths passing through S, which are precisely those paths not passing through N, have one less black node. Now all paths in the subtree rooted by P have the same number of black nodes, but one fewer than the paths that do not pass through P, so requirement 4 may still be violated. Recursive repair on the higher level is required, i.e., let N := P and continue the repair process until the new N is root(Delete case 2).

Delete case 2 #
As the recusive repair process goes up, if N is root, it means one black node has been removed from every path, so the RB-properties are preserved. The black height of the tree decreases by 1. in this case the deletion is complete
Delete case 3 #
The sibling S is red, so P and the nephews C and D have to be black. A dir-rotation at P turns S into N’s grandparent. Then after reversing the colors of P and S, the path through N is still short one black node. But N has a red parent P and a black sibling S, so the transformations in cases D4, D5, or D6 are able to restore the RB-shape.
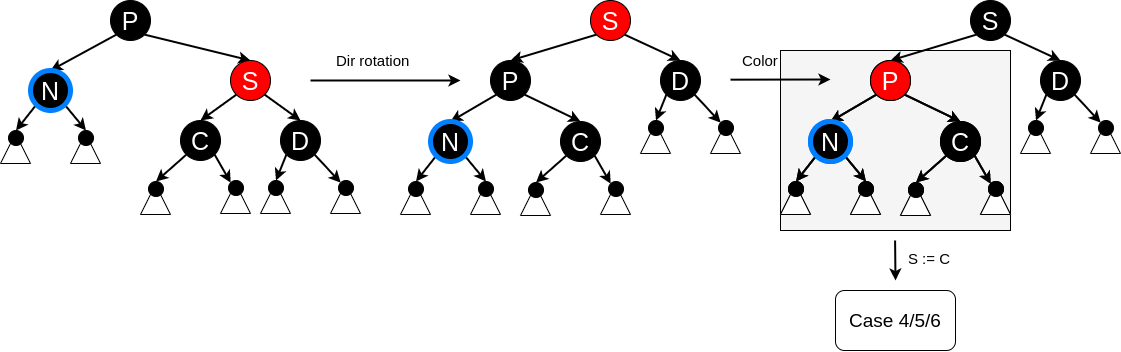
Delete case 4 #
The sibling S and S’s children are black, but P is red. Exchanging the colors of S and P does not affect the number of black nodes on paths going through S, but it does add one to the number of black nodes on paths going through N, making up for the deleted black node on those paths. in this case the deletion is complete.
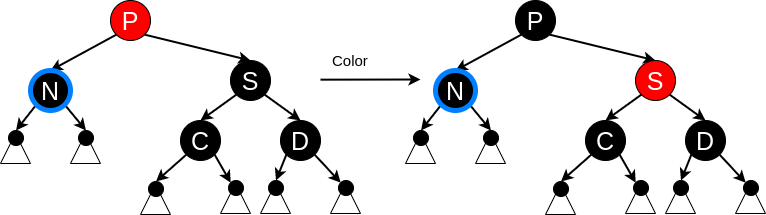
Delete case 5 #
The sibling S is black, S’s close child C is red, and S’s distant child D is black. After a (1-dir)-rotation at S the nephew C becomes S’s parent and N’s new sibling. Then we exchange the color of S and C. All paths still have the same number of black nodes, but now N has a black sibling whose distant child is red, so the constellation is fit for case D6. Neither N nor its parent P are affected by this transformation, and P may be red or black (⭕ in the table above).
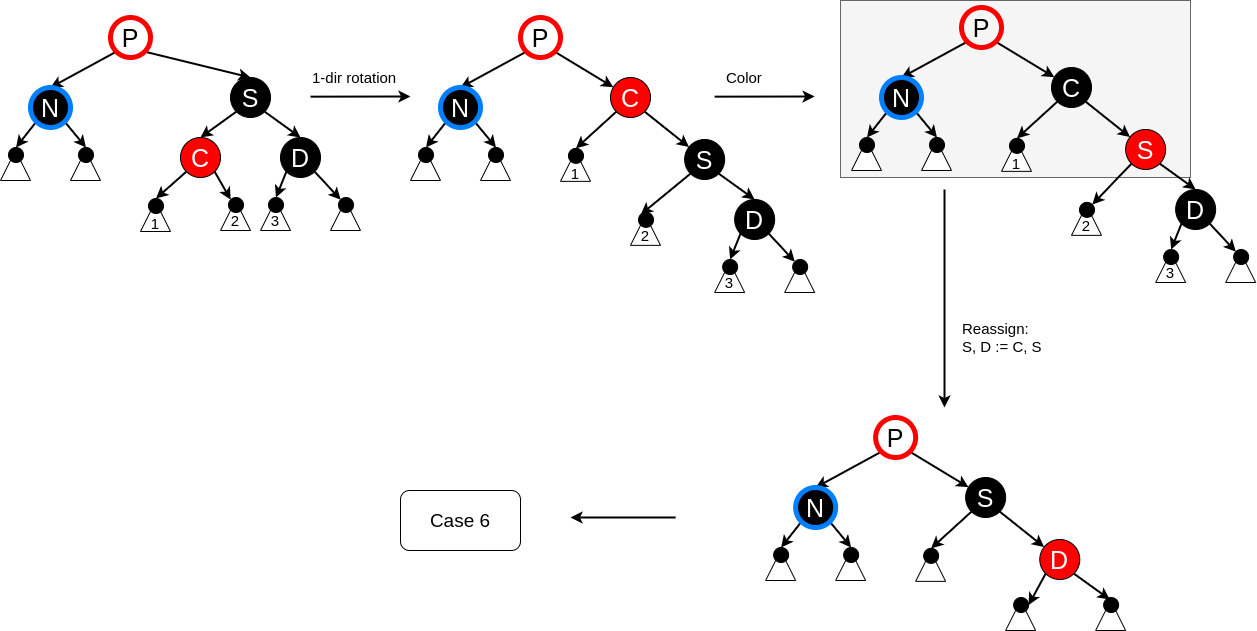
Delete case 6 #
The sibling S is black, S’s distant child D is red. After a dir-rotation at P the sibling S becomes the parent of P and `S’s distant child D. The colors of P and S are exchanged, and D is made black. The subtree still has the same color at its root, namely either red or black (RedOrBlackNode.svg in the diagram), which refers to the same color both before and after the transformation. This way requirement 3 is preserved. The paths in the subtree not passing through N (i.o.w. passing through D and node 3 in the diagram) pass through the same number of black nodes as before, but N now has one additional black ancestor: either P has become black, or it was black and S was added as a black grandparent. Thus, the paths passing through N pass through one additional black node, so that requirement 4 is restored and the total tree is in RB-shape.