Level order traversal of a binary tree #
Given a binary tree, print its nodes level by level, i.e., print all nodes of level 1 first, followed by nodes of level 2 and so on… Print nodes for any level from left to right.
Introduction #
We have already discussed preorder, inorder, and postorder traversals of the binary tree, which are nothing but variations of depth–first order of a Tree. Trees can also be traversed in level order, where we visit every node on a level before going to a lower level. This search is referred to as level order traversal or Breadth–first search (BFS), as the search tree is broadened as much as possible on each depth before going to the next depth.
For example, the level order traversal for the following tree is 1, 2, 3, 4, 5, 6, 7:
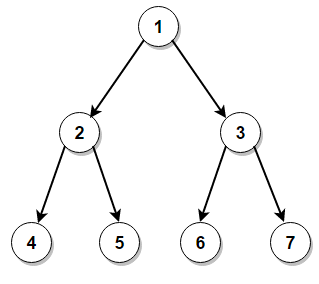
Solution #1 #
A simple solution is to print all nodes of level 1 first, followed by level 2, until level h, where h is the tree’s height. We can print all nodes present in a level by modifying the preorder traversal on the tree. This is demonstrated below in C++.
#include <iostream>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Function to print all nodes of a given level from left to right
bool printLevel(Node* root, int level)
{
if (root == nullptr) {
return false;
}
if (level == 1)
{
cout << root->key << " ";
// return true if at least one node is present at a given level
return true;
}
bool left = printLevel(root->left, level - 1);
bool right = printLevel(root->right, level - 1);
return left || right;
}
// Function to print level order traversal of a given binary tree
void levelOrderTraversal(Node* root)
{
// start from level 1 — till the height of the tree
int level = 1;
// run till printLevel() returns false
while (printLevel(root, level)) {
level++;
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
levelOrderTraversal(root);
return 0;
}
Output:
15 10 20 8 12 16 25
The time complexity of the above solution is O(n2), where n is the total number of nodes in the binary tree. The auxiliary space required by the program is O(h) for the call stack, where h is the height of the tree.
Solution #2 #
We can reduce the time complexity to O(n) by using extra space. Following is a pseudocode for a simple queue-based level order traversal, which requires space proportional to the maximum number of nodes at a given depth. It can be as much as half the total number of nodes.
levelorder(root)
q —> empty queue
q.enqueue(root)
while (not q.isEmpty())
node —> q.dequeue()
visit(node)
if (node.left <> null)
q.enqueue(node.left)
if (node.right <> null)
q.enqueue(node.right)
The algorithm can be implemented as follows in C++:
#include <iostream>
#include <list>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Function to print level order traversal of a given binary tree
void levelOrderTraversal(Node* root)
{
// base case
if (root == nullptr) {
return;
}
// create an empty queue and enqueue the root node
list<Node*> queue;
queue.push_back(root);
// pointer to store the current node
Node* curr = nullptr;
// loop till queue is empty
while (queue.size())
{
// process each node in the queue and enqueue their
// non-empty left and right child
curr = queue.front();
queue.pop_front();
cout << curr->key << " ";
if (curr->left) {
queue.push_back(curr->left);
}
if (curr->right) {
queue.push_back(curr->right);
}
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
levelOrderTraversal(root);
return 0;
}
Output:
15 10 20 8 12 16 25
The time complexity of the above solution is O(n) and requires O(n) extra space, where n is the size of the binary tree.
Solution #3 #
We can also solve this problem by using hashing. The idea is to traverse the tree in a preorder fashion and store every node and its level in a multimap using the level number as a key. Finally, print all nodes corresponding to every level starting from the first level. We can also traverse the tree in inorder or postorder fashion.
Following is the implementation of the above approach in C++
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Traverse the tree in a preorder fashion and store nodes in a map
// corresponding to their level
void preorder(Node* root, int level, auto &map)
{
// base case: empty tree
if (root == nullptr) {
return;
}
// insert the current node and its level into the map
map[level].push_back(root->key);
// recur for the left and right subtree by increasing the level by 1
preorder(root->left, level + 1, map);
preorder(root->right, level + 1, map);
}
// Recursive function to print level order traversal of a given binary tree
void levelOrderTraversal(Node* root)
{
// create an empty map to store nodes between given levels
unordered_map<int, vector<int>> map;
// traverse the tree and insert its nodes into the map
// corresponding to their level
preorder(root, 1, map);
// iterate through the map and print all nodes between given levels
for (int i = 1; map[i].size() > 0; i++)
{
cout << "Level " << i << ": ";
for (int j: map[i]) {
cout << j << " ";
}
cout << endl;
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
root->right->right->right = new Node(30);
levelOrderTraversal(root);
return 0;
}
Output:
Level 1: 15
Level 2: 10 20
Level 3: 8 12 16 25
Level 4: 30
The time complexity of the above solution is O(n) and requires O(n) extra space, where n is the size of the binary tree.
Solution #4 #
Iterative level order traversal to levels line by line
#include <iostream>
#include <queue>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Iterative method to do level order traversal line by line
void levelOrderTraversal(Node* root)
{
if(root == nullptr) {
return;
}
// create an empty queue for level order traversal
queue<Node *> q;
// enqueue Root and initialize height
q.push(root);
while (q.empty() == false)
{
// nodeCount (queue size) indicates number
// of nodes at current level.
int nodeCount = q.size();
// Dequeue all nodes of current level and
// Enqueue all nodes of next level
while (nodeCount > 0)
{
Node *node = q.front();
cout << node->key << " ";
q.pop();
if (node->left != nullptr){
q.push(node->left);
}
if (node->right != nullptr){
q.push(node->right);
}
nodeCount--;
}
cout << endl;
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
root->right->right->right = new Node(30);
levelOrderTraversal(root);
return 0;
}
Output:
Level 1: 15
Level 2: 10 20
Level 3: 8 12 16 25
Level 4: 30
Solution #5 #
Iterative level order traversal to levels line by line using two queues.
#include <iostream>
#include <queue>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Iterative method to do level order traversal line by line using two queues.
void levelOrderTraversal(Node* root)
{
if(root == nullptr) {
return;
}
// create two queues for level order traversal
queue<Node *> qa, qb;
// pushing first level node into first queue
qa.push(root);
while (!qa.empty() || !qb.empty())
{
while (!qa.empty())
{
// Pushing left child of current node in
// first queue into second queue
if (qa.front()->left != NULL)
qb.push(qa.front()->left);
// pushing right child of current node
// in first queue into second queue
if (qa.front()->right != NULL)
qb.push(qa.front()->right);
cout << qa.front()->key << " ";
qa.pop();
}
cout << endl;
while (!qb.empty())
{
// pushing left child of current node
// in second queue into first queue
if (qb.front()->left != NULL)
qa.push(qb.front()->left);
// pushing right child of current
// node in second queue into first queue
if (qb.front()->right != NULL)
qa.push(qb.front()->right);
cout << qb.front()->key << " ";
qb.pop();
}
cout << endl;
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
root->right->right->right = new Node(30);
levelOrderTraversal(root);
return 0;
}
Output:
Level 1: 15
Level 2: 10 20
Level 3: 8 12 16 25
Level 4: 30
Solution #6 #
Iterative level order traversal to levels line by line
#include <iostream>
#include <queue>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int key;
Node *left, *right;
Node(int key)
{
this->key = key;
this->left = this->right = nullptr;
}
};
// Iterative method to do level order traversal line by line
void levelOrderTraversal(Node* root)
{
if(root == nullptr) {
return;
}
// create an empty queue for level order traversal
queue<Node *> q;
// enqueue Root and initialize height
q.push(root);
q.push(nullptr);
Node *curr;
while (q.size() > 1)
{
curr = q.front();
q.pop();
// condition to check occurrence of next level.
if (curr == nullptr) {
q.push(nullptr);
cout << endl;
} else {
// pushing left child of current node.
if(curr->left){
q.push(curr->left);
}
// pushing right child of current node.
if(curr->right) {
q.push(curr->right);
}
cout << curr->key << " ";
}
}
}
int main()
{
Node* root = new Node(15);
root->left = new Node(10);
root->right = new Node(20);
root->left->left = new Node(8);
root->left->right = new Node(12);
root->right->left = new Node(16);
root->right->right = new Node(25);
root->right->right->right = new Node(30);
levelOrderTraversal(root);
return 0;
}
Output:
Level 1: 15
Level 2: 10 20
Level 3: 8 12 16 25
Level 4: 30