Inorder Tree Traversal – Iterative and Recursive #
Given a binary tree, write an iterative and recursive solution to traverse the tree using inorder traversal in C++.
Introduction #
Unlike linked lists, one-dimensional arrays, and other linear data structures, which are traversed in linear order, trees can be traversed in multiple ways in depth–first order (preorder, inorder, and postorder) or breadth–first order (level order traversal). Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth–first search. In this post, inorder tree traversal is discussed in detail.
Traversing a tree involves iterating over all nodes in some manner. As the tree is not a linear data structure, there can be more than one possible next node from a given node, so some nodes must be deferred, i.e., stored in some way for later visiting. The traversal can be done iteratively where the deferred nodes are stored in the stack, or it can be done by recursion, where the deferred nodes are stored implicitly in the call stack.
For traversing a (non-empty) binary tree in a inorder fashion, we must do these three things for every node n starting from the tree’s root:
- Recursively traverse its left subtree. When this step is finished, we are back at n again.
- Process n itself.
- Recursively traverse its right subtree. When this step is finished, we are back at n again.
In normal inorder traversal, we visit the left subtree before the right subtree. If we visit the right subtree before visiting the left subtree, it is referred to as reverse inorder traversal.
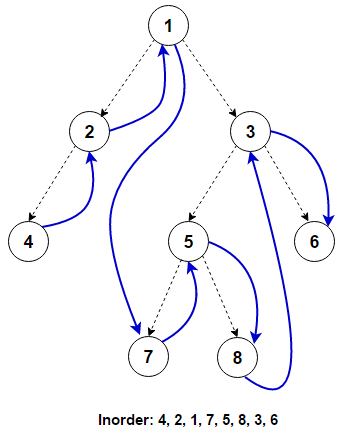
Recursive Implementation #
As we can see, before processing any node, the left subtree is processed first, followed by the node, and the right subtree is processed at last. These operations can be defined recursively for each node. The recursive implementation is referred to as a Depth–first search (DFS), as the search tree is deepened as much as possible on each child before going to the next sibling.
Following is the C++ program that demonstrates it:
#include <iostream>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
// Recursive function to perform inorder traversal on the tree
void inorder(Node* root)
{
// return if the current node is empty
if (root == nullptr) {
return;
}
// Traverse the left subtree
inorder(root->left);
// Display the data part of the root (or current node)
cout << root->data << " ";
// Traverse the right subtree
inorder(root->right);
}
int main()
{
/* Construct the following tree
1
/ \
/ \
2 3
/ / \
/ / \
4 5 6
/ \
/ \
7 8
*/
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
inorder(root);
return 0;
}
Iterative Implementation #
To convert the above recursive procedure into an iterative one, we need an explicit stack. Following is a simple stack-based iterative algorithm to perform inorder traversal:
iterativeInorder(node)
s —> empty stack
while (not s.isEmpty() or node != null)
if (node != null)
s.push(node)
node —> node.left
else
node —> s.pop()
visit(node)
node —> node.right
The algorithm can be implemented as follows in C++:
#include <iostream>
#include <stack>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
// Iterative function to perform inorder traversal on the tree
void inorderIterative(Node* root)
{
// create an empty stack
stack<Node*> stack;
// start from the root node (set current node to the root node)
Node* curr = root;
// if the current node is null and the stack is also empty, we are done
while (!stack.empty() || curr != nullptr)
{
// if the current node exists, push it into the stack (defer it)
// and move to its left child
if (curr != nullptr)
{
stack.push(curr);
curr = curr->left;
}
else {
// otherwise, if the current node is null, pop an element from the stack,
// print it, and finally set the current node to its right child
curr = stack.top();
stack.pop();
cout << curr->data << " ";
curr = curr->right;
}
}
}
int main()
{
/* Construct the following tree
1
/ \
/ \
2 3
/ / \
/ / \
4 5 6
/ \
/ \
7 8
*/
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
inorderIterative(root);
return 0;
}
The time complexity of the above solutions is O(n), where n is the total number of nodes in the binary tree. The space complexity of the program is O(n) as the space required is proportional to the height of the tree, which can be equal to the total number of nodes in the tree in worst-case for skewed trees.