Postorder Tree Traversal - Iterative and Recursive #
Given a binary tree, write an iterative and recursive solution to traverse the tree using postorder traversal in C++
Introduction #
Unlike linked lists, one-dimensional arrays, and other linear data structures, which are traversed in linear order, trees can be traversed in multiple ways in depth–first order (preorder, inorder, and postorder) or breadth–first order (level order traversal). Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth–first search. In this post, postorder tree traversal is discussed in detail.
Traversing a tree involves iterating over all nodes in some manner. As the tree is not a linear data structure, there can be more than one possible next node from a given node, so some nodes must be deferred, i.e., stored in some way for later visiting. The traversal can be done iteratively where the deferred nodes are stored in the stack, or it can be done by recursion, where the deferred nodes are stored implicitly in the call stack.
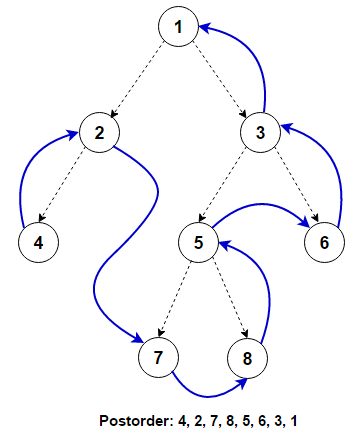
For traversing a (non-empty) binary tree in a postorder fashion, we must do these three things for every node n starting from the tree’s root:
- Recursively traverse its left subtree. When this step is finished, we are back at n again.
- Recursively traverse its right subtree. When this step is finished, we are back at n again.
- Process n itself.
In normal postorder traversal, visit the left subtree before the right subtree. If we visit the right subtree before visiting the left subtree, it is referred to as reverse postorder traversal.
Recursive Implementation #
As we can see, before processing any node, the left subtree is processed first, followed by the right subtree, and the node is processed at last. These operations can be defined recursively for each node. The recursive implementation is referred to as a Depth–first search (DFS), as the search tree is deepened as much as possible on each child before going to the next sibling.
#include <iostream>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
// Recursive function to perform postorder traversal on the tree
void postorder(Node* root)
{
// if the current node is empty
if (root == nullptr) {
return;
}
// Traverse the left subtree
postorder(root->left);
// Traverse the right subtree
postorder(root->right);
// Display the data part of the root (or current node)
cout << root->data << " ";
}
int main()
{
/* Construct the following tree
1
/ \
/ \
2 3
/ / \
/ / \
4 5 6
/ \
/ \
7 8
*/
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
postorder(root);
return 0;
}
Iterative Implementation - Two Stacks #
To convert the above recursive procedure into an iterative one, we need an explicit stack. Following is a simple stack-based iterative algorithm to perform postorder traversal:
iterativePostorder(node)
s —> empty stack
t —> output stack
while (not s.isEmpty())
node —> s.pop()
t.push(node)
if (node.left <> null)
s.push(node.left)
if (node.right <> null)
s.push(node.right)
while (not t.isEmpty())
node —> t.pop()
visit(node)
The algorithm can be implemented as follows in C++
#include <iostream>
#include <stack>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
// Iterative function to perform postorder traversal on the tree
void postorderIterative(Node* root)
{
// return if the tree is empty
if (root == nullptr) {
return;
}
// create an empty stack and push the root node
stack<Node*> s;
s.push(root);
// create another stack to store postorder traversal
stack<int> out;
// loop till stack is empty
while (!s.empty())
{
// pop a node from the stack and push the data into the output stack
Node* curr = s.top();
s.pop();
out.push(curr->data);
// push the left and right child of the popped node into the stack
if (curr->left) {
s.push(curr->left);
}
if (curr->right) {
s.push(curr->right);
}
}
// print postorder traversal
while (!out.empty())
{
cout << out.top() << " ";
out.pop();
}
}
int main()
{
/* Construct the following tree
1
/ \
/ \
2 3
/ / \
/ / \
4 5 6
/ \
/ \
7 8
*/
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
postorderIterative(root);
return 0;
}
The time complexity of the above solutions is O(n), where n is the total number of nodes in the binary tree. The space complexity of the program is O(n) as the space required is proportional to the height of the tree, which can be equal to the total number of nodes in the tree in worst-case for skewed trees.
Iterative Implementation - One Stack #
The idea is to move down to leftmost node using left pointer. While moving down, push root and root’s right child to stack. Once we reach leftmost node, print it if it doesn’t have a right child. If it has a right child, then change root so that the right child is processed before.
The algorithm can be implemented as follows in C++
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
// Data structure to store a binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
// Iterative function to perform postorder traversal on the tree
void postorderIterative(Node* root)
{
// return if the tree is empty
if (root == nullptr) {
return;
}
vector<int> result;
// create an empty stack.
stack<Node*> s;
do
{
// Move to leftmost node
while (root)
{
// Push root's right child and then root to stack.
if (root->right)
s.push(root->right);
s.push(root);
// Set root as root's left child
root = root->left;
}
// Pop an item from stack and set it as root
root = s.top();
s.pop();
// If the popped item has a right child and the right child is not
// processed yet, then make sure right child is processed before root
if (!s.empty() && root->right && s.top() == root->right)
{
s.pop(); // remove right child from stack
s.push(root); // push root back to stack
root = root->right; // change root so that the right child is processed next
} else { // Else print root's data and set root as NULL
result.push_back(root->data);
root = nullptr;
}
} while (!s.empty());
// print postorder traversal
for(auto item: result) {
cout << item << " ";
}
}
int main()
{
/* Construct the following tree
1
/ \
/ \
2 3
/ / \
/ / \
4 5 6
/ \
/ \
7 8
*/
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->right->left = new Node(5);
root->right->right = new Node(6);
root->right->left->left = new Node(7);
root->right->left->right = new Node(8);
postorderIterative(root);
return 0;
}