Check if a graph contains a cycle in 3 ways #
Cycle detection is an application that is widely used in deadlock detection, wait-for graph, or dependencies analysis, this post is implementing cycle detection in 3 ways.
Introduction #
Given a connected undirected graph, check if it contains any cycle or not.
For example, the following graph contains a cycle 2-5-10-6-2:
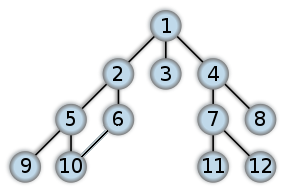
1. Using BFS #
When we do a Breadth–first search (BFS) from any vertex v in an undirected graph, we may encounter a cross-edge that points to a previously discovered vertex that is neither an ancestor nor a descendant of the current vertex. Each “cross edge” defines a cycle in an undirected graph. If the cross edge is x —> y and y is already discovered, we have a path from v to y (or from y to v since the graph is undirected), where v is the starting vertex of BFS. So, we can say that we have a path v ~~ x ~ y ~~ v that forms a cycle. (Here, ~~ represents one more edge in the path, and ~ represents a direct edge).
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Node to store vertex and its parent info in BFS
struct Node {
int v, parent;
};
// Perform BFS on the graph starting from vertex `src` and
// return true if a cycle is found in the graph
bool BFS(Graph const &graph, int src, int n)
{
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n);
// mark the source vertex as discovered
discovered[src] = true;
// create a queue for doing BFS and
// enqueue source vertex
queue<Node> q;
q.push({src, -1});
// loop till queue is empty
while (!q.empty())
{
// dequeue front node and print it
Node node = q.front();
q.pop();
// do for every edge (v, u)
for (int u: graph.adjList[node.v])
{
if (!discovered[u])
{
// mark it as discovered
discovered[u] = true;
// construct the queue node containing info
// about vertex and enqueue it
q.push({ u, node.v });
}
// `u` is discovered, and `u` is not a parent
else if (u != node.parent)
{
// we found a cross-edge, i.e., the cycle is found
return true;
}
}
}
// no cross-edges were found in the graph
return false;
}
int main()
{
// initialize edges
vector<Edge> edges =
{
{0, 1}, {0, 2}, {0, 3}, {1, 4}, {1, 5}, {4, 8},
{4, 9}, {3, 6}, {3, 7}, {6, 10}, {6, 11}, {5, 9}
// edge {5, 9} introduces a cycle in the graph
};
// total number of nodes in the graph (0 to 11)
int n = 12;
// build a graph from the given edges
Graph graph(edges, n);
// Perform BFS traversal in connected components of a graph
if (BFS(graph, 0, n)) {
cout << "The graph contains a cycle";
}
else {
cout << "The graph doesn't contain any cycle";
}
return 0;
}
Output: The graph contains a cycle
2. Using DFS #
The following graph contains a cycle 8—9—11—12—8:
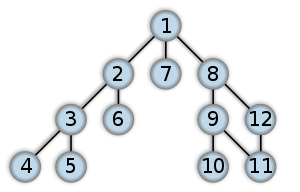
When we do a Depth–first search (DFS) from any vertex v in an undirected graph, we may encounter a back-edge that points to one of the ancestors of the current vertex v in the DFS tree. Each “back edge” defines a cycle in an undirected graph. If the back edge is x —> y, and y is the ancestor of node x, we have a path from y to x. So, we can say that we have a path y ~~ x ~ y that forms a cycle. (Here, ~~ represents one more edge in the path, and ~ represents a direct edge).
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Perform DFS on the graph and returns true if any back-edge is found in the graph
bool DFS(Graph const &graph, int v, vector<bool> &discovered, int parent)
{
// mark the current node as discovered
discovered[v] = true;
// do for every edge (v, w)
for (int w: graph.adjList[v])
{
// if `w` is not discovered
if (!discovered[w])
{
if (DFS(graph, w, discovered, v)) {
return true;
}
}
// if `w` is discovered, and `w` is not a parent
else if (w != parent)
{
// we found a back-edge (cycle)
return true;
}
}
// No back-edges were found in the graph
return false;
}
int main()
{
// initialize edges
vector<Edge> edges =
{
{0, 1}, {0, 6}, {0, 7}, {1, 2}, {1, 5}, {2, 3},
{2, 4}, {7, 8}, {7, 11}, {8, 9}, {8, 10}, {10, 11}
// edge (10, 11) introduces a cycle in the graph
};
// total number of nodes in the graph (0 to 11)
int n = 12;
// build a graph from the given edges
Graph graph(edges, n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n);
// Perform DFS traversal from the first vertex
if (DFS(graph, 0, discovered, -1)) {
cout << "The graph contains a cycle";
}
else {
cout << "The graph doesn't contain any cycle";
}
return 0;
}
Output: The graph contains a cycle
The time complexity of the above solutions is O(V + E), where V and E are the total number of vertices and edges in the graph, respectively.
3. Using Disjoint-Set(Uniou-Find Algorithm) #
The following graph contains a cycle 8—9—11—12—8:

We strongly recommend watch the first 10 mins of this video to get a clear picture.
Complete Algorithm:
1. Create disjoint sets for each vertex of the graph.
2. For every edge u, v in the graph
i) Find the root of the sets to which elements u and v belongs.
ii) If both u and v have the same root in disjoint sets, a cycle is found.
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges) {
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// A class to represent a disjoint set
class DisjointSet
{
unordered_map<int, int> parent;
public:
// perform MakeSet operation
void MakeSet(int n)
{
// create `n` disjoint sets (one for each vertex)
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// Find the root of the set in which element `k` belongs
int Find(int k)
{
// if `k` is root
if (parent[k] == k) {
return k;
}
// recur for the parent until we find the root
return Find(parent[k]);
}
// Perform Union of two subsets
void Union(int a, int b)
{
// find the root of the sets in which elements `x` and `y` belongs
int x = Find(a);
int y = Find(b);
parent[x] = y;
}
};
// Returns true if the graph has a cycle
bool findCycle(Graph const &graph, int n)
{
// initialize Main class
DisjointSet ds;
// create a singleton set for each element of the universe
ds.MakeSet(n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n);
// consider every edge (u, v)
for (int u = 0; u < n; u++)
{
// Recur for all adjacent vertices
for (int v: graph.adjList[u])
{
if (discovered[v]) {
continue;
}
// find the root of the sets to which elements `u` and `v` belongs
int x = ds.Find(u);
int y = ds.Find(v);
// if both `u` and `v` have the same parent, the cycle is found
if (x == y) {
return true;
}
ds.Union(x, y);
}
discovered[u] = true;
}
return false;
}
// Union–find algorithm for cycle detection in a graph
int main()
{
// vector of graph edges
vector<Edge> edges =
{
{0, 1}, {0, 6}, {0, 7}, {1, 2}, {1, 5}, {2, 3},
{2, 4}, {7, 8}, {7, 11}, {8, 9}, {8, 10}, {10, 11}
// edge (10, 11) introduces a cycle in the graph
};
// total number of nodes in the graph (labelled from 0 to 11)
int n = 12;
// build a graph from the given edges
Graph graph(edges, n);
if (findCycle(graph, n)) {
cout << "Cycle Found";
}
else {
cout << "No Cycle Found";
}
return 0;
}
Output: Cycle Found
The time complexity of the Union and Find operation is O(n) in the worst case, where n is the total number of vertices in the graph.