Breadth-First Search (BFS) – Iterative and Recursive Implementation #
Breadth–first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’) and explores the neighbor nodes first before moving to the next-level neighbors.
Introduction #
The following graph shows the order in which the nodes are discovered in BFS:
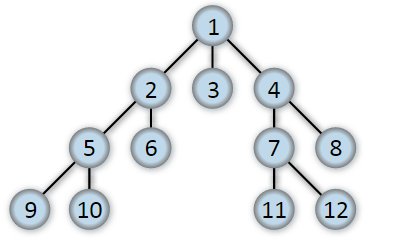
Breadth–first search (BFS) is a graph traversal algorithm that explores vertices in the order of their distance from the source vertex, where distance is the minimum length of a path from the source vertex to the node as evident from the above example.
Applications of BFS #
- Copying garbage collection, Cheney’s algorithm.
- Finding the shortest path between two nodes u and v, with path length measured by the total number of edges (an advantage over depth–first search).
- Testing a graph for bipartiteness.
- Minimum Spanning Tree for an unweighted graph.
- Web crawler.
- Finding nodes in any connected component of a graph.
- Ford–Fulkerson method for computing the maximum flow in a flow network.
- Serialization/Deserialization of a binary tree vs. serialization in sorted order allows the tree to be reconstructed efficiently.
Iterative Implementation of BFS #
The non-recursive implementation of BFS is similar to the non-recursive implementation of DFS but differs from it in two ways:
- It uses a queue instead of a stack.
- It checks whether a vertex has been discovered before pushing the vertex rather than delaying this check until the vertex is dequeued.
The algorithm can be implemented as follows in C++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Perform BFS on the graph starting from vertex `v`
void BFS(Graph const &graph, int v, vector<bool> &discovered)
{
// create a queue for doing BFS
queue<int> q;
// mark the source vertex as discovered
discovered[v] = true;
// enqueue source vertex
q.push(v);
// loop till queue is empty
while (!q.empty())
{
// dequeue front node and print it
v = q.front();
q.pop();
cout << v << " ";
// do for every edge (v, u)
for (int u: graph.adjList[v])
{
if (!discovered[u])
{
// mark it as discovered and enqueue it
discovered[u] = true;
q.push(u);
}
}
}
}
int main()
{
// vector of graph edges as per the above diagram
vector<Edge> edges = {
{1, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6}, {5, 9},
{5, 10}, {4, 7}, {4, 8}, {7, 11}, {7, 12}
// vertex 0, 13, and 14 are single nodes
};
// total number of nodes in the graph (labelled from 0 to 14)
int n = 15;
// build a graph from the given edges
Graph graph(edges, n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n, false);
// Perform BFS traversal from all undiscovered nodes to
// cover all connected components of a graph
for (int i = 0; i < n; i++)
{
if (discovered[i] == false)
{
// start BFS traversal from vertex `i`
BFS(graph, i, discovered);
}
}
return 0;
}
Output: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Recursive Implementation of BFS #
The recursive algorithm can be implemented as follows in C++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// Data structure to store a graph edge
struct Edge {
int src, dest;
};
// A class to represent a graph object
class Graph
{
public:
// a vector of vectors to represent an adjacency list
vector<vector<int>> adjList;
// Graph Constructor
Graph(vector<Edge> const &edges, int n)
{
// resize the vector to hold `n` elements of type `vector<int>`
adjList.resize(n);
// add edges to the undirected graph
for (auto &edge: edges)
{
adjList[edge.src].push_back(edge.dest);
adjList[edge.dest].push_back(edge.src);
}
}
};
// Perform BFS recursively on the graph
void recursiveBFS(Graph const &graph, queue<int> &q, vector<bool> &discovered)
{
if (q.empty()) {
return;
}
// dequeue front node and print it
int v = q.front();
q.pop();
cout << v << " ";
// do for every edge (v, u)
for (int u: graph.adjList[v])
{
if (!discovered[u])
{
// mark it as discovered and enqueue it
discovered[u] = true;
q.push(u);
}
}
recursiveBFS(graph, q, discovered);
}
int main()
{
// vector of graph edges as per the above diagram
vector<Edge> edges = {
{1, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6}, {5, 9},
{5, 10}, {4, 7}, {4, 8}, {7, 11}, {7, 12}
// vertex 0, 13, and 14 are single nodes
};
// total number of nodes in the graph (labelled from 0 to 14)
int n = 15;
// build a graph from the given edges
Graph graph(edges, n);
// to keep track of whether a vertex is discovered or not
vector<bool> discovered(n, false);
// create a queue for doing BFS
queue<int> q;
// Perform BFS traversal from all undiscovered nodes to
// cover all connected components of a graph
for (int i = 0; i < n; i++)
{
if (discovered[i] == false)
{
// mark the source vertex as discovered
discovered[i] = true;
// enqueue source vertex
q.push(i);
// start BFS traversal from vertex `i`
recursiveBFS(graph, q, discovered);
}
}
return 0;
}
Output: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
The time complexity of BFS traversal is O(V + E), where V and E are the total number of vertices and edges in the graph, respectively. Please note that O(E) may vary between O(1) and O(V2), depending on how dense the graph is.
Also See:
Breadth First Search (BFS) – Interview Questions & Practice Problems(https://www.techiedelight.com/bfs-interview-questions/)